Variables aléatoires réelles
--- Introduction ---
Ce module regroupe pour l'instant 10 exercices sur les
variables aléatoires réelles.
Les exercices "Construction d'une v.a. de loi discrète",
"Description des lois classiques", "Réalisation d'une variable aléatoire"
et "Transformation d'une v.a. à densité" portent à la fois sur des lois continues
et des lois discrètes. L'exercice "Propriétés d'une loi et transformation linéaire"
s'applique à n'importe quel type de v.a. réelles.
L'exercice "Des identités utilisant l'espérance" ne s'applique qu'aux v.a. positives.
Les autres exercices concernent les lois à densité.
L'exercice "Calculer avec une loi à densité" est paramétrable (voir ci-dessous).
On trouvera d'autres exercices sur les lois de v.a. réelles par exemple dans
les modules : OEF loi d'une v.a. discrète,
OEF Loi normale et
OEF Représentation graphique de lois classiques.
Aires et loi normale
La courbe représente la densité de la loi normale d'espérance et d'écart-type .
xrange , yrange -0.1, hline 0,0,black arrow ,0,-0.1,0,10,black arrow 0,-0.1,0,,10,black text gray, -0.1,0,,0
On note
une variable aléatoire de loi normale d'espérance et d'écart-type .
L'aire du domaine colorié est la probabilité d'un des événements ci-dessous, lequel ?
L'aire du domaine colorié est la probabilité de l'évènement .
La probabilité de l'événement est :
Calculer avec une loi à densité
- Pour quelle valeur du paramètre
, la fonction
suivante est-elle une densité de probabilité ?
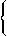 |
| si |
|
|
| sinon | |
La valeur de
est :
Bonne réponse ! Il faut et il suffit que
- Soit
une variable aléatoire de densité
. Calculer la probabilité que l'événement
se réalise.
Bonne réponse ! P(
) = .
- Déterminer .
=
Densité et transformations d'une v.a.
La courbe suivante représente la densité d'une variable aléatoire
. ![]()
Cliquez sur la courbe qui représente la densité de la variable aléatoire
.
Des identités utilisant l'espérance
Soit
une variable aléatoire à valeurs dans
. Compléter l'identité suivante en entrant une fonction de
) =
Description des lois classiques
- La loi est une loi :
.
- Une variable aléatoire
de loi est à valeurs dans :
.
NB : sélectionner la réponse la plus précise
-
pour tout
,
=
Calcul avec la loi normale
Soit
une variable aléatoire de loi normale d'espérance et de variance .
Donner l'expression de la probabilité de l'événement à l'aide de la fonction de répartition
de la loi normale
prise uniquement en des valeurs positives ou nulles. Exemple : si
suit la loi
, la probabilité que
soit inférieure à -1 s'écrira
.
P() =
Propriétés d'une loi et transformation linéaire
Soit
une variable aléatoire réelle qui admet un moment d'ordre 2 fini. On suppose que son espérance est
et est
.
On pose
.
Complétez : - P(
[ ; ] ) =
P(
[
;
] )
P(
[ ; ] )
- L'espérance de
est
et est
.
Réalisation d'une variable aléatoire
On a tiré une réalisation d'une variable aléatoire de loi . On a obtenu . Si on recommence cette expérience, quelle est la probabilité d'obtenir une valeur ?
Construction d'une v.a. de loi discrète
On considère une variable aléatoire
de loi uniforme sur l'intervalle [0,1]. - Déterminer les valeurs possibles pour la variable aléatoire
c'est-à-dire déterminer les valeurs qui sont prises avec une probabilité strictement positive (on séparera les valeurs par des virgules).
Valeurs possibles :
Bonne réponse : les valeurs possibles pour
sont bien
.
- Déterminer la loi de la variable aléatoire
.
Transformation d'une v.a. à densité
Soit
une variable aléatoire de loi . On considère la variable aléatoire
= .
1- Quel type de variable aléatoire est
?
est une v.a. à
Bonne réponse !
est une variable aléatoire .
2- Compléter l'expression suivante de la fonction
, pour que
soit la fonction de répartition de
| si |
|
|
| |
| | si |
|
|
|
| | si |
|
|
Compléter l'expression suivante qui définit la loi de
| si
est entier et |
|
|
| |
| si
n'est pas entier | |
| | ou si
| |
| | ou si
| |
NB : on écrira inf pour + et -inf pour -
et -inf pour -
2- Bonne réponse ! La fonction de répartition
de
est définie par :
pour tout
.
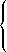 |
| si
|
|
| si
|
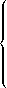 |
| si
|
|
| si
|
|
| si
|
3- Compléter l'expression suivante de la fonction
afin que ce soit une densité pour
pour tout
.
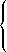 |
|
si |
|
|
| sinon | |
2- Bonne réponse ! On a bien
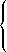 |
| si
est un entier et si |
|
| si
|
| si |
|
|
| sinon |
3- Compléter l'expression suivante de la fonction
, afin que ce soit la fonction de répartition de
|
|
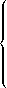 |
|
si |
|
|
| si
|
|
| si
|
NB : on écrira floor(x) pour désigner la partie entière de
.
The most recent version
Cette page n'est pas dans son apparence habituelle parce que
WIMS n'a pas pu reconnaître votre navigateur web.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne
sont pas des fichiers
HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE.
Il est inutile pour vous de les ramasser par un programme robot.
- Description: collection d'exercices sur les variables aléatoires réelles (lois continues et lois discrètes). interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, mathematics,probability, random_variable, probability_distribution, events, proba, densité, loi continue, loi discrète, fonction de répartition, espérance, moment, variance, réalisation d'une variable aléatoire
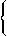
 et -inf pour -
et -inf pour -