OEF Géométrie du plan complexe
--- Introduction ---
Ce module regroupe pour l'instant 11 exercices sur les isométries et transformations affines du plan complexe.
Isométries en complexes
On se place dans le plan affine euclidien muni d'un repère orthonormé direct d'origine
. La transformation
qui à un point
d'affixe
associe le point
d'affixe
donné par
.
est une isométrie
est une isométrie puisque
est de la forme
avec
avec
.
Plus précisément
est une
.
est une .
L'affixe de son vecteur est
.
Préciser ses éléments caractéristiques :
Son centre a pour affixe
et son angle a pour mesure
.
Donner la mesure principale de l'angle en radian et pour
, écrire pi.
Préciser ses éléments caractéristiques :
Son axe passe par le point d'affixe
et fait un angle de mesure
avec l'axe des
.
Donner la mesure principale de l'angle en radian et pour
, écrire pi.
Alors
est la composée d'une réflexion d'axe
et d'une translation de vecteur
qui dirige
.
L'axe
passe par le point d'affixe
, l'affixe du vecteur
est
.
Points fixes d'une isométrie
On se place dans le plan affine euclidien muni d'un repère orthonormé direct d'origine
et on considère la transformation
qui à un point
d'affixe
associe le point
d'affixe
donné par
.
Que peut-on dire de l'isométrie
?
Rectangle
Si
et
sont des points du plan d'affixes
et
, trouver l'affixe de points
et
tels que
soit un rectangle dont la longueur d'un côté soit le de l'autre.
Nature des transformations complexes
La transformation qui à un point
d'affixe
associe le point
d'affixe
donné par
est une
Donner la réponse la plus précise.
est une similitude directe
et plus précisément une
. Préciser ses éléments caractéristiques :
| centre |
translation |
angle | rapport |
|
|
|
|
Similitudes en complexes
On se place dans le plan affine euclidien muni d'un repère orthonormé direct d'origine
. La transformation
qui à un point
d'affixe
associe le point
d'affixe
donné par
.
est une
est une qui n'est pas une isométrie puisque
est de la forme
avec
avec
.
Son rapport vaut
.
L'affixe de son centre est
.
Son angle a pour mesure
.
Cette transformation est-elle une homothétie ?
Donner la mesure principale de l'angle en radian et pour
, écrire pi.
Son axe passe par le centre et fait un angle de mesure
avec l'axe des
.
Donner la mesure principale de l'angle en radian et pour
, écrire pi.
Composition de similitudes
Soit
la similitude qui à un point
d'affixe
associe le point
d'affixe
donné par
Soit
la similitude qui à un point
d'affixe
associe le point
d'affixe
donné par
Calculer la transformation
qui envoie
sur
sur
par son écriture complexe
=
+
Figures et similitudes
Soit
un tel que
=
.
=
et tel que l'angle en
soit de mesure  /.
l'angle en
soit de mesure
.
Alors
est l'image de
par une similitude directe
/.
l'angle en
soit de mesure
.
Alors
est l'image de
par une similitude directe de centre
, d'angle
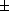
et de rapport
En effet,
est l'image de
par une similitude directe de centre
, d'angle
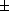
et de rapport
.
-
=
* exp(
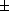
) * (
-
.)
Triangle isocèle
Si
et
sont des points du plan d'affixe
et
, trouver l'affixe d'un point
tel que le triangle
soit isocèle en
et d'angle
égal à degrés.
Triangle équilatéral
Si
et
sont des points du plan d'affixes
et
, trouver l'affixe d'un point
tel que le triangle
soit équilatéral.
Triangle rectangle isocèle
Si
et
sont des points du plan d'affixes
et
, trouver l'affixe d'un point
tel que le triangle
soit rectangle isocèle en
.
Triangle rectangle isocèle2
Si
et
sont des points du plan d'affixe
et
, trouver l'affixe d'un point
tel que le triangle
soit rectangle isocèle en
.
The most recent version
Cette page n'est pas dans son apparence habituelle parce que
WIMS n'a pas pu reconnaître votre navigateur web.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne
sont pas des fichiers
HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE.
Il est inutile pour vous de les ramasser par un programme robot.
- Description: collection d'exercices sur les isométries et similitudes dans le plan complexe. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, mathematics, algebra, geometry, rotation,similarities,translation,isometries, complex_number, complex_plane
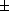 et de rapport
et de rapport
 /.
l'angle en
soit de mesure
.
Alors
est l'image de
par une similitude directe
/.
l'angle en
soit de mesure
.
Alors
est l'image de
par une similitude directe  et de rapport
et de rapport
 et de rapport
.
et de rapport
.  ) * (
-
.)
) * (
-
.)